写像

写像も集合の言葉で書き表せるのだ

<$> \gdef\id{\operatorname{id}} <$>

定義

皆さんおなじみの「関数」が「写像」になって帰ってきたのだ！

$f=(F,A,B)$ が以下をみたすとき、「$A$ から $B$ への写像である」といい、$f:A\to B$ と書くのだ:

• $F\in 2^{A\times B}$
• $\forany{a\in A}\uexst{b\in B}(a,b)\in F$

またこのとき $A$ を $f$ の始域、$B$ を $f$ の終域というのだ

日本語で書くのだ。$F$ は $A\times B$ の部分集合で、また各 $a\in A$ にたいして $(a,b)\in F$ となる $b\in B$ がただ一つだけ存在するのだ

$\uexst x p(x)\colonLrarr \exist x,\ p(x)\land\forall y,\ p(y)\Rarr x=y$ ($p(x)$ は命題関数) のことだったのを思い出してほしいのだ。煩雑だから $\uexist$ って書いてるだけだし、「ただ一つ存在する」って考えておけば十分なのだ

このままではあんまり帰ってきた感じがしないので、次の記法を導入するのだ:

$f=(F,A,B)$ を関数とするのだ。このとき各 $a\in A$ に対して $(a,b)\in F$ となる $b\in B$ がただ一つだけ存在するので、$f(a)=b$ と定めるのだ

命題的に言うと、$b=f(a)\Lrarr (a,b)\in F$ なのだ。これによって $F$ に直接言及しなくても $(a,b)\in F$ の話がしやすくなったのだ

また、これを $a\xmapsto f b$ と書くこともあるのだ。さらに、ちゃんとした表現ではないけど $f$ は $a$ を $b$ に飛ばすと言ったりするのだ

写像のイメージ

見た目にも関数っぽくなったと思うのだ。写像のことを関数とも言うのだ

具体例

では写像の具体例を見ていくのだ。定義をよく見返しながら当てはまっているか確認してほしいのだ

$f=\Bigl(\bigl\{(0,1),(2,3)\bigr\},\{0,2\},\{1,3\}\Bigr)$ は写像なのだ。$f(0)=1,\ f(2)=3$ と書けるのだ

ちょっと難しいけど、
$g=\Bigl(\bigl\{(0,1),(1,2),(2,3),(3,4),\ldots\bigr\},\N,\N\Bigr)$ も写像なのだ

$g(0)=1,g(1)=2,\ldots,g(n)=n+1$ なのが見てわかると思うのだ

他にも関数っぽくないけど、
$h=\Bigl(\bigl\{(0,\{0\}),(1,\{1,2\})\bigr\},\{0,1\},2^\N\Bigr)$ も写像になるのだ

$h(1)=\{1,2\}$ って式はなんだか不思議にも見えるのだ

写像じゃない例も見てみるのだ

$i=\Bigl(\bigl\{(0,0)\bigr\},\{0,1,2\},\{0,1\}\Bigr)$ は写像じゃないのだ。$i(1)$ となる $\{0,1\}$ の元が存在しないからなのだ

$j=\Bigl(\bigl\{(0,0),(1,1),(2,1),(3000000,0)\bigr\},\{0,1,2\},\{0,1\}\Bigr)$ も明らかに写像じゃないのだ。$(3000000,0)\notin\{0,1,2\}\times\{0,1\}$ なのだ

写像の作り方

いつもこんな書き方で数学者は写像を定義しているのかって？　とんでもないのだ。こんな書き方してたらなにもせずに一生が終わるのだ

基本的な書き方

一番基本的な書き方は $(a$ の式$)\in B$ に対して $f(a)\coloneqq(a$ の式$)$ なのだ。そりゃそうなのだ。中学生くらいからずっとこうやって書いてきたのだ

でも数学は厳密だから、$f$ がどこからどこへの写像なのかを省略することは滅多にないのだ

$f:A\to B$ と合わせて次のように書くのだ:

$f:$	$A$	$\to$	$B$
	$\in$		$\in$
	$a$	$\mapsto$	$(a$ の式$)$

$f:$	$A$	$\to$	$B$
	$a$	$\mapsto$	$(a$ の式$)$

$f: A\ni a\mapsto (a$ の式$)\in B$

$f: A\to B,\ f(a)=(a$ の式$)$

絶対に $f:A\to B$ の表記は省かないと思ってほしいのだ*1

この記事では $f:A\ni a\mapsto (a$ の式$)\in B$ の書き方を採用するのだ。理由はブログで書きやすいからなのだ。数学者はいつだって面倒くさがりやなのだ

実際には上のように書いて:
$f=\Bigl(\bigl\{p\in A\times B\mid \exst{a\in A}p=(a,(a$ の式$))\bigr\},A,B\Bigr)$
を意味するのだ。これがちゃんと写像になっていることを証明してみるんだけど、$(a$ の式$)$ という曖昧な書き方に強く依存しちゃうからちょっと歯切れが悪いのだ:

まず上で $p\in A\times B$ って書いてあるから最初の条件はクリアなのだ

そして $\any a\in A$ にたいして $(a$ の式$)$ は一通りの値しか返さないのだ

詳しく言えば $(a$ の式$)$ は必ずなにか値を持っているはずだし、$b=(a$ の式$)$ とおけば $\any c=(a$ の式$)$ に対してどう見ても $b=c$ だから $\uexist$ の定義にも従うのだ

でも $(a$ の式$)$ を $expr(a)$ とか書いたら関数みたいで気持ち悪いのでここらで我慢してほしいのだ

これで関数をきれいに書けるようになったのだ

例えば上の $g=\Bigl(\bigl\{(0,1),(1,2),(2,3),(3,4),\ldots\bigr\},\N,\N\Bigr)$ は、
$g:\N\ni n\mapsto n+1\in\N$ って簡潔に書けるのだ

式があればそれを関数にできる、って言い換えることもできるのだ。関数とはそういうものだったはずなのだ

同じように $f:\R\ni x\mapsto x^2\in\R$ や $g:\R\ni x\mapsto e^x\in\R$ などおなじみの関数も写像になるのだ

他にも $h:\N\ni n\mapsto \{m\in\N\mid m< n\}\in 2^\N$ なんてのも写像なのだ

$h(5)=\{0,1,2,3,4\}$ みたいにちゃんと計算できてるのだ

$\uexist$ から写像を作る

「ただ一つ存在する」ってのが重要だったので、そこから写像を作ることもできるのだ

例えば、ある命題関数*2 $p(a,b)$ に対して $\forany{a\in A}\uexst{b\in B}p(a,b)$ だったとするのだ

このとき $f=\Bigl(\bigl\{q\in A\times B\mid \exst{a\in A,\ b\in B}p(a,b)\land q=(a,b)\bigr\},A,B\Bigr)$ は写像になるのだ

このように「ただ一つ存在するので、これを関数 $f:A\to B$ と定める」みたいな書き方ができるのだ

上で定義したものが写像になることを証明してみるのだ:

$\bigl\{q\in A\times B\mid \exst{a\in A,\ b\in B}p(a,b)\land q=(a,b)\bigr\}\eqqcolon F$ とおくのだ

まずその定義より $F\in 2^{A\times B}$ なのだ

次に $\any a\in A$ をとるのだ。「$\uexst{b\in B}(a,b)\in F$」を示せばいいのだ

$p(a,b)$ の定義より $\uexst{b\in B}p(a,b)$ なのだ

$q\coloneqq(a,b)\in A\times B$ とおくのだ

$p(a,b)\land q=(a,b)$ だから $F$ の定義より $(a,b)=q\in F$ となのだ

次に $(a,\any c)\in F$ をとるのだ。このとき、$F$ の定義より $p(a,c)$ なのだ。$b$ の定義より $b=c$ となり、一つしか存在しないことが言えたのだ

ほとんど $p(a,b)$ の性質しか使ってないのだ

well-defined 性

実際には $\uexist$ から写像を作るよりも $p(a,b)$ を $p(a,f(a))$ の形で書いて写像の概形を与え、その後で $\forany{a\in A}\uexst{b\in B}p(a,b)$ を示すことのほうが多いのだ

例えば、$f:\N\to\N,\ f(n)-n=1$ と書いた上で $\forany{n\in\N}\uexst{m\in\N}m-n=1$ を証明するのだ。このときの $\forany{n\in\N}\uexst{m\in\N}m-n=1$、上での $\forany{a\in A}\uexst{b\in B}p(a,b)$ を well-defined 性、というのだ

直訳すれば「ちゃんと定義できているか」「うまく定義されているか」などになると思うんだけど、そのまま well-defined って言うことの方が多いのだ

写像周辺のこまごまとした定義

写像の集合

写像の集合、なんてのも考えられるのだ:

集合 $A,B$ に対して「$A$ から $B$ への写像全体の集合」

<$>\begin{aligned} \operatorname{Map}(A,B)&\coloneqq\bigl\{f\in 2^{A\times B}\times\{A\}\times\{B\}\mid f:A\to B\bigr\} \end{aligned}<$>

が定義されるのだ。$\operatorname{Map}(A,B)$ のことを $B^A,\ \mathcal{F}(A,B),\ A\to B$ と書いたりもするのだ

等号

写像が等しいかは単に集合の順序対として等しいかでしかないのだ。でも一応:

$\forany{f,g:A\to B}f=g\Lrarr \forany{a\in A}f(a)=g(a)$

で写像が等しいことを見たりするのだ。もちろん $f$ も $g$ も $A\to B$ だからこれが言えるんであって $g:A\to C$ とかだったら当然ダメなのだ

合成

写像同士の計算が定義されるのだ:

$f:A\to B,\ g:B\to C$ に対して、$g\circ f:A\ni a\mapsto g(f(a))\in C$ を定め、「$g$ と $f$ の合成」と呼ぶのだ

一般に $g\circ f=f\circ g$ とは限らないのだ。

<$>\begin{aligned} f&:\N\ni n\mapsto n+1\in\N\\ g&:\N\ni n\mapsto n^2\in\N \end{aligned}<$>

を考えれば $(g\circ f)(1)=4\ne 2=(f\circ g)(1)$ からすぐにわかるのだ

また、すぐわかる性質として $f:A\to B,\ g:B\to C,\ h:C\to D$ を用意したとき $h\circ(g\circ f)=(h\circ g)\circ f$ なのだ:

どちらも $A\to D$ なのはわかるので $\any a\in A$ をとれば:

<$>\begin{aligned} \bigl(h\circ(g\circ f)\bigr)(a)&=h\bigl((g\circ f)(a)\bigr)\\ &=h\Bigl(g\bigl(f(a)\bigr)\Bigr)\\ &=(h\circ g)\bigl(f(a)\bigr)\\ &=\bigl((h\circ g)\circ f\bigr)(a) \end{aligned}<$>

で、$a$ は任意より $h\circ(g\circ f)=(h\circ g)\circ f$ なのだ

簡単に $h\circ g\circ f$ なんて書いたりすることもあるのだ

恒等写像

集合 $A$ に対して $\id_A:A\ni a\mapsto a\in A$ を「恒等写像」と呼ぶのだ。他にも $1_A$ とか $\operatorname{Id}_A$ とか書かれるのだ

自明な性質として $f:A\to B$ に対し $f\circ \id_A=f,\ \id_B\circ f=f$ が成り立つのだ

逆写像

逆数みたいな概念なのだ。$2\times 0.5=1$ になるのと同じ感じで:

$f:A\to B,\ g:B\to A$ が $g\circ f=\id_A,\ f\circ g=\id_B$ のとき、「$g$ は $f$ の逆写像である」というのだ。また、この $g$ は存在すればただ一つであることが知られているので、$f^{-1}$ と書かれるのだ

実数なら $xy=yx$ だけど関数だと $f\circ g=g\circ f$ なんてわけにはいかないので、きちんと $f\circ g$ と $g\circ f$ がどちらも恒等写像になることを慎重に確かめる必要があるのだ

また自明なこととして $g$ が $f$ の逆写像であるとき、$f$ は $g$ の逆写像なのだ

逆写像があっても 1 つだけ、というのは以下のように証明されるのだ:

$g:B\to A,\ h:B\to A$ が共に $f:A\to B$ の逆写像だとするのだ
このとき

<$>\begin{aligned} g&=g\circ\id_B\\ &=g\circ(f\circ h)\\ &=(g\circ f)\circ h\\ &=\id_A\circ h\\ &=h \end{aligned}<$>

より $g=h$ なのだ

では、逆写像の例を挙げるのだ。まず、$A$ に対して $\id_A$ は $\id_A$ の逆写像なのだ

他にも

<$>\begin{aligned} f&:\{0,1,2,3\}\ni n\mapsto n+1\in\{1,2,3,4\}\\ g&:\{1,2,3,4\}\ni n\mapsto n-1\in\{0,1,2,3\} \end{aligned}<$>

は互いに逆写像の関係なのだ

普通の関数なら

<$>\begin{alignedat}{2} &h&:\R\ni x\mapsto x+1\in\R\\ &i&:\R\ni x\mapsto x-1\in\R \end{alignedat}<$>

なんかも逆写像の関係になっているのだ

じゃあ、逆写像じゃない例を挙げてみるのだ

<$>\begin{alignedat}{4} f:&\,&\{-1,0,1\}&\ni\,& n&\mapsto n^2&\in\,&\{0,1\}\\ g:&&\{0,1\}&\ni\,& n&\mapsto n&\in\,&\{-1,0,1\} \end{alignedat}<$>

は $f\circ g=\id_{\{0,1\}}$ だけど $(g\circ f)(-1)=1$ だから逆写像じゃないのだ

単射と全射

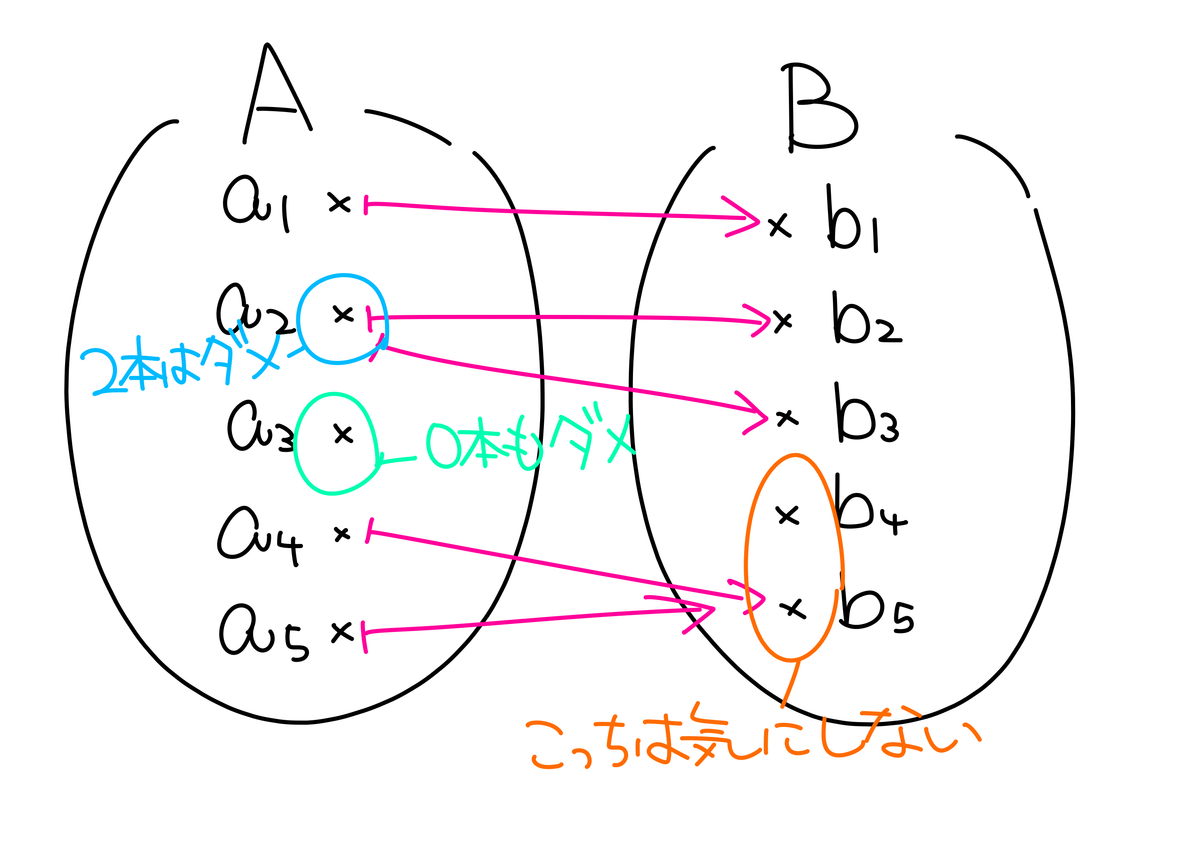
全射と単射はイメージが難しい概念として知られているのだ。雑な図と共にお送りするのだ

単射

$f: A\to B$ が次をみたすとき、単射(injection, inj.)というのだ:

• $\forany{a_1,a_2\in A}f(a_1)=f(a_2)\Rarr a_1=a_2$

よく「行き先がつぶれない」って表現されるのだ。対偶をとった $\forany{a_1,a_2\in A}a_1\ne a_2\Rarr f(a_1)\ne f(a_2)$ のほうがわかりやすいかもしれないのだ

単射の図

単射じゃない図

単射な例として簡単なのは $f: \{1,2,3\}\ni n\mapsto n\in\{1,2,3,4,5\}$ なのだ。そのまま突っ込んでるだけだから $1,2,3$ の行き先が同じものには絶対ならないのだ

おなじみの実数だけの関数で考えると

<$>\begin{alignedat}{2} f&:\R\ni x\mapsto x^3&\,\in\R\\ g&:\R\ni x\mapsto e^x&\,\in\R \end{alignedat}<$>

などが単射なのだ。実際に $f(x_1)=f(x_2)$ を考えてみると、

<$>\begin{aligned} f(x_1)&=f(x_2)\\ x_1^3&=x_2^3\\ x_1^3-x_2^3&=0\\ (x_1-x_2)(x_1^2+x_1 x_2+x_2^2)&=0\\ (x_1-x_2)\bigl((x_1+\frac{x_2}2)^2+\frac{3 x_2^2}4\bigr)&=0\\ x_1-x_2&=0\\ x_1&=x_2 \end{aligned}<$>

と同値に式変形できて単射が示せるのだ

単射じゃない例は簡単に作れるのだ。$f:\{1,2,3,4\}\ni n\mapsto 1\in\{1\}$ がそうなのだ。もはや $f(1)=f(2)=f(3)=f(4)$ なのだ。全部つぶれてるのだ

実数だと $f:\R\ni x\mapsto x^2\in\R$ なんかがそれなのだ。$f(1)=1=f(-1)$ なのだ

全射

$f:A\to B$ が次をみたすとき、全射(surjection, surj.)というのだ:

• $\forany{b\in B}\exst{a\in A}f(a)=b$

矢印が $B$ の元全部に向かっているのを全射、と呼ぶのだ

全射の図

全射じゃない図

全射の例として $f:\{1,2,3,4\}\ni n\mapsto 1\in\{1\}$ が挙げられるのだ。全ての $\{1\}$ の元 (といっても $1$ しかないけど) に $f(n)=1$ となるような $n$ が存在してるのだ。具体的には $n=1$ とかなのだ

実数の話だと $f:\R\ni x\mapsto x^3\in\R$ は全射なのだ。証明はちょっと割愛なのだ

全射じゃない例は $f:\{1,2,3\}\ni n\mapsto 1\in\{1,2\}$ が挙げられるのだ。さっきの全射な例の $\{1\}$ が $\{1,2\}$ に変わっただけなのに全射じゃなくなっちゃったのだ。$f(n)=2$ となる $n\in\{1,2,3\}$ は存在しないことがわかるのだ。このように全射は写像の終域に依存する概念なのだ

実数だと $f:\R\ni x\mapsto e^x\in\R$ がそれなのだ。$f(x)=-1$ となる $x\in\R$ は存在しないのだ

全単射

$f: A\to B$ が全射で単射なとき、全単射(bijection, bij.)というのだ

全単射は非常にお行儀がいいことで知られているのだ。例としては $f:\{1,2,3,4,5\}\ni n\mapsto 6-n\in\{1,2,3,4,5\}$ などが挙げられるのだ

他にも $g:\{1,2,3,4\}\ni n\mapsto n+1\in\{2,3,4,5\}$ とか。始域と終域の元の個数が一致していることに気づくと思うのだ。これは重要なことなのだ

$h:\R\ni x\mapsto 2x\in\R$ も全単射なのだ

全単射と逆写像の関係

全単射と逆写像にはある単純な関係があることが知られているのだ:

$f:A\to B$ に対して、次の 2 つは同値なのだ:

• $f:\text{bij.}$
• $\exst{g:B\to A}g$ は $f$ の逆写像

これはすごいことなのだ。全射で単射だったら逆写像が存在してしまうのだ！　簡単な条件からしっかりした写像ができてしまうというのは非常に面白い現象だと思うのだ。数学で初めて出会う非自明な性質なのだ！

では証明といくのだ:

「$(\exst{g:B\to A}g$ は $f$ の逆写像$)\Rarr f:\text{bij.}$」を示すのだ

まず $f$ の逆写像 $g$ の存在を仮定するのだ

$\forany{a_1,a_2\in A}f(a_1)=f(a_2)$ をとれば $a_1=g(f(a_1))=g(f(a_2))=a_2$ となって単射が言えたのだ

$\any a\in A$ をとって $b\coloneqq g(a)\in B$ とすれば $f(b)=f(g(a))=a$ となって全射も言えたのだ

「$f:\text{bij.}\Rarr\exst{g:B\to A}g$ は $f$ の逆写像」を示すのだ

さっきの $\uexist$ から写像を作る より、$\forany{b\in B}\uexst{a\in A}f(a)=b$ が言えれば写像が構成できるのだ。実際に証明してみるのだ

$\any b\in B$ をとるのだ。全射より $\exst{a\in A}f(a)=b$ なのだ。次に $\anyst{c\in C}f(c)=b$ をとるのだ。すると $f:\text{inj.}$ より $a=c$ だから示せたのだ

以上より $\forany{b\in B}\uexst{a\in A}f(a)=b$ が言えたのでこの $a$ を $g(b)$ に対応させて写像 $g:B\to A$ を作るのだ

すると、定義より明らかに $f(g(b))=b$ だから $f\circ g=\id_B$ なのだ

さらに $\any a\in A$ に対して

<$>\begin{aligned} f\Bigl(g\bigl(f(a)\bigr)\Bigr)&=(f\circ g)\bigl(f(a)\bigr)\\ &=\id_B\bigl(f(a)\bigr)\\ &=f(a) \end{aligned}<$>

で、$f:\text{inj.}$ より $a=g\bigl(f(a)\bigr)$、すなわち $g\circ f=\id_A$ なのだ

これで $g$ は $f$ の逆写像であることが示せたのだ

像と逆像

写像で集合の元をいっぺんに飛ばすと新しい集合が作れるのだ

像

$f:A\to B$ と集合 $X_A\subset A$ に対して
$f(X_A)\coloneqq\{b\in B\mid \exst{a\in X_A}f(a)=b\}$ を $f$ による $X_A$ の像と呼ぶのだ

写像を矢印で表した図だと、$X_A$ から出る矢印の右側を集めた集合のことなのだ

$f:\R\ni x\mapsto x^2\in\R$ と $X=\{x\in\R\mid -1\leq x\leq 2\}$ に対して $f(X)=\{x\in\R\mid 0\leq x\leq 4\}$ なのだ

値域

関数 $f:A\to B$ に対してその行き先全体の集合
$\operatorname{Im}(f)\coloneqq f(A)=\{b\in B\mid\exst{a\in A}f(a)=b\}$ が定義されるのだ

例えば $f:\R\ni x\mapsto x^2\in\R$ の値域は $\{x\in\R\mid x\geq 0\}$ だし、$g:\N\ni n\mapsto n+1\in\N$ の値域は $\{n\in\N\mid n\geq 1\}$ なのだ

逆像

$f:A\to B$ と集合 $X_B\subset B$ に対して
$f^{-1}(X_B)\coloneqq\{a\in A\mid f(a)\in X_B\}$ を $f$ による $X_B$ の逆像と呼ぶのだ

さっきの逆なのだ。$X_B$ に飛ぶ矢印の左側全体なのだ。$f(a)\in X_B$ を $\exst{b\in X_B}f(a)=b$ って書けば像の定義と似ているのがわかるはずなのだ。$f^{-1}$ って書いたけどこれは逆写像のことじゃないから気をつけるのだ。紛らわしい記号だけどみんな使ってるから我慢してほしいのだ。さっきの $f$ と $X$ に対して $f^{-1}(X)=\{x\in\R\mid -\sqrt 2\leq x\leq \sqrt 2\}$ なのだ

写像の色々な形

関数以外でもみんな意識せずに写像を使っていることがあるのだ

族

これは ZFC からちょっと離れた概念だから、正確に語るのは難しいのだ

ある集合 $\Lambda, X$ とその上の写像 $x:\Lambda\to X$ に対して、
$(x_\lambda)_{\lambda\in\Lambda}$ を(添字づけられた)族と呼ぶのだ

ただし $x_\lambda\coloneqq x(\lambda)$ で、この記法を添字、$\Lambda$ を添字集合と呼ぶのだ

また、族それ自体は集合としても写像としても見ることがあるのだ。

さらに集合として見る性質上終域よりも値域のほうが圧倒的に重要なので、終域が省略されることも多いのだ

集合としてみればこれは $\operatorname{Im}(x)$ のことで、写像としては $x$ そのものを指すのだ。さらに色々曖昧な記法が登場しがちなので気をつけて読んでほしいのだ

例えば写像 $x$ を $(x_\lambda=f(\lambda))_{\lambda\in\lambda}$ の形で定義してしまうこともあるし、終域を $(x_\lambda)_{\lambda\in\Lambda}\subset X$ なんて指定することもあるのだ。合わせて $(x_\lambda=f(\lambda))_{\lambda\in\Lambda}\subset X$ なのだ。写像を定義しているのに、$\subset$ は集合としてみたときの記法なのだ。とってもややこしいけど一応直感的ではあると思うのだ

添字を使えば $X$ の元を扱うときに $\Lambda$ の元の性質を使えるからとてもうれしいのだ

数列 (点列)

$\N$ には「順番」という性質があるから、それを利用したのが数列または点列なのだ。例えば $(a_n=2^{-n})_{n\in\N}\subset\R$ なんて書いたりするのだ。これが実数の数列として使えるのは見ればわかるのだ。例えば $a_2=\frac 14$ だし、高校での数列と形も一緒なのだ

順番をつけることで収束の概念も簡単に捉えられるのだ

小うるさい記法の話

ただ、この解釈だとちょっと問題があるのだ。なぜなら収束先を $a_n\xrightarrow[n\to\infty]{}a$ のように書くことがあって、もとの写像とされている $a:\N\to\R$ と衝突するからなのだ

ただの写像として $a$ を定義するんじゃなくて $a_n$ の表記のみを認める $a_\bullet:\N\to A$ という写像だと考えればいいのだ。黒丸で引数の位置を指定する記法なのだ。ただこれも収束先の表現である $a_\infty$ と衝突するのだ……。まあ臨機応変に行くのだ。なにも絶対記法を統一しなきゃいけないってことはないし

部分列

数列 $(a_n)_{n\in\N}$ が $(x_n)_{n\in\N}$ の部分列であるとは、以下のときを言うのだ:

• $\exst{m:\N\to\N}a_n=x_{m(n)}\land\anyst{i,j\in\N}i< j,\ m(i)< m(j)$

また、このとき $(a_n)_{n\in\N}\subset(x_n)_{n\in\N}$ と書くのだ

順番が入れ替わることなく元が引っこ抜かれたと思って欲しいのだ

例えば $(a_n=2^{-n})_{n\in\N}$ にたいして $(b_n=2^{-2n})_{n\in\N}$ は部分列になっているのだ。$m(n)=2n$ とすればわかると思うのだ

でも $(c_n=2^{-(n-5)^2})_{n\in\N}$ は $(a_n=2^{-n})_{n\in\N}$ の部分列になっていないのだ。これは並びを見れば直感的に

<$>\frac 1{2^{25}},\frac 1{2^{16}},\frac 1{2^9},\frac 1{16},\frac 12,\ldots<$>

となって順番が逆になってるな、と思えると思うのだ

実際に $m(n)=2^{-(n-5)^2}$ は $m(0)>m(1)$ だからすぐにちがうって言えるのだ

あと、もはや集合としての包含関係ではないけど $\subset$ と書くのだ。すごく紛らわしいけど、数列に関して言えばかなり直感的な表現であることがわかると思うのだ

添字づけられた集合族

集合の集合を集合族というのだ。集合の集合はたくさん出てくるから、早めになれておいた方がいいのだ。全部の集合に $A,B,C,\ldots,Z,AA,AB,\ldots$ なんて名前つけてられないから、添字づけることが多いのだ

「集合族 $(X_\lambda)_{\lambda\in\Lambda}$ が……」って表現することも多いのだ

和集合の書き方

添字づけられた集合族 $(X_\lambda)_{\lambda\in\Lambda}$ の和集合を $\displaystyle\bigcup_{\lambda\in\Lambda}X_\lambda$ と書くのだ

また、命題関数 $p(\lambda)$ と $\Lambda$ の部分集合 $A=\{\lambda\in\Lambda\mid p(\lambda)\}$ について $\bigcup X(A)$ を $\displaystyle\bigcup_{\lambda\in\Lambda,\ p(\lambda)}X_\lambda$ と便利に書けるのだ

共通部分

共通部分も同じように $\displaystyle\bigcap_{\lambda\in\Lambda}X_\lambda$ と書くのだ

直積集合

直積集合をこれで定義することがあるのだ。まず添字づけられた集合 $(X_\lambda)_{\lambda\in\Lambda}$ を用意するのだ。これの直積集合の元を次で定義するのだ:

$\displaystyle\prod_{\lambda\in\Lambda}X_\lambda\coloneqq\left\{p:\Lambda\to\bigcup_{\lambda\in\Lambda}X_\lambda\mathrel{}\middle|\mathrel{}\forany{\lambda\in\Lambda}p(\lambda)\in X_\lambda\right\}$

写像 $p$ の終域は適当に広くとっただけだから気にしなくていいのだ。問題は $\forany{\lambda\in\Lambda}p(\lambda)\in X_\lambda$ の方なのだ

難しいと思うので、$\Lambda=\{0,1\}$ として見てみるのだ。このとき $\displaystyle\any p\in\prod_{\lambda\in\Lambda}X_\lambda$ に対して、$p(0)\in X_0,\ p(1)\in X_1$ がわかるのだ。なんとなく有限直積集合に似てるのだ

この方法のすごいところは任意の集合族に対して直積集合がとれちゃうことなのだ。だから無限直積集合なるものが定義できるのだ

例えば $X=\displaystyle\prod_{n\in\N}\{x\in\R\mid 0< x<\frac 1n\}$ みたいな集合がつくれちゃうのだ！　この場合は $x\in X$ を数列と捉えて、$(x_n)_{n\in\N}\subset\R\st 0< x_n<\frac 1n$ 全体の集合だと思えばいいのだ

次回は選択公理と濃度なのだ。お楽しみに

*1:ずーっと $\R\to\R$ しか扱わないから毎回書きたくないとか、どこからどこへのかに関わらず写像全体の議論をしたいときとか、例外はあるのだ

*2:命題関数は関数じゃないの？　って思うかもしれないけど、これは命題を一般的に扱うために定めたメタ的なもの、ただの略記みたいなものだと思ってほしいのだ。現実にはちゃんと命題ごとに毎回議論してる、って体でお願いするのだ